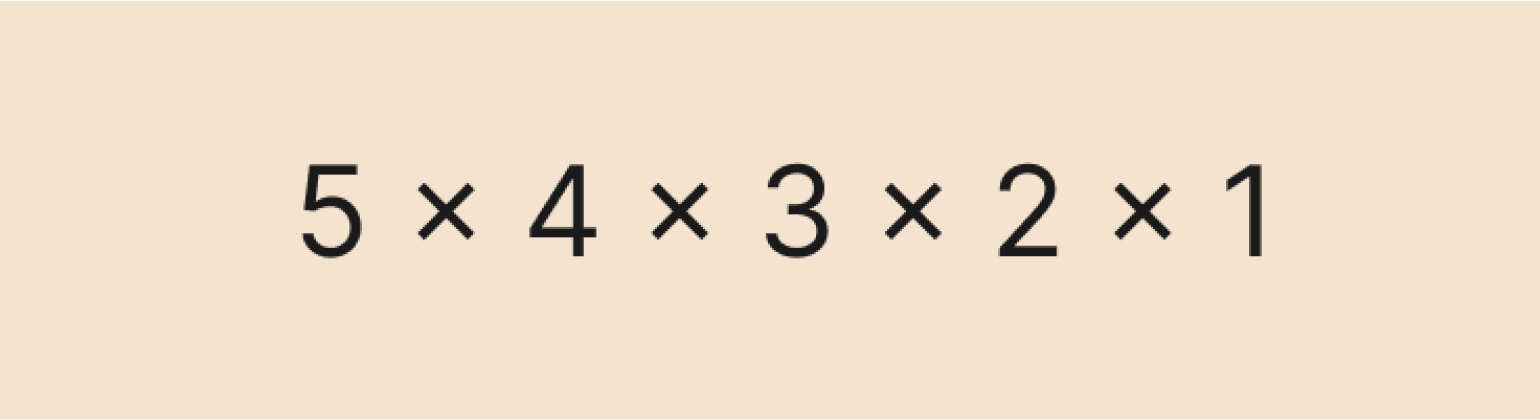
Математика – замечательная наука, в которой каждое правило имеет свое объяснение. Одним из самых интересных и запутанных правил является вычисление факториала, особенно когда речь идет о нулевом факториале. Почему же 0 факториал равен 1? Давайте разберемся в этом.
Факториал числа n обозначается как n! и равен произведению всех натуральных чисел от 1 до n. Например, 5! равен 1 * 2 * 3 * 4 * 5 = 120. Также существуют рекуррентные формулы для вычисления факториала, в которых факториал числа n выражается через факториал числа n-1.
Теперь рассмотрим случай с нулевым факториалом. По определению факториала, факториал числа 0 равен произведению всех натуральных чисел от 1 до 0. На первый взгляд это может показаться непонятным, ведь 0 участников в произведении приводит к нулевому результату. Однако, по мнению математиков, это произведение необходимо определить равным 1.
Одним из аргументов в пользу того, что 0 факториал равен 1, является рекуррентная формула вычисления факториала. При использовании этой формулы при n = 1 мы получим: 1! = 1 * (1 — 1)! = 1 * 0!. Следовательно, 0! должен быть равен 1, так как иначе рекуррентная формула не будет выполняться.
Иными словами, нулевой факториал является базовым случаем для рекуррентной формулы вычисления факториала и его равенство 1 – это соглашение, которое позволяет сохранить правильность формулы для всех чисел n.
Факториал числа
Факториал числа обозначается символом !. Например, факториал числа 5 равен 5! = 5 * 4 * 3 * 2 * 1 = 120.
Факториалы широко используются в математике, статистике и программировании, особенно в комбинаторике и теории вероятностей.
Факториал 0 является специальным случаем и определен как равный 1. Математически это можно объяснить следующим образом: если у нас нет ни одного объекта, то есть ни одного способа упорядочить или переставить эти объекты, поэтому количество вариантов равно 1.
Например:
- 0! = 1
- 1! = 1 * 0! = 1 * 1 = 1
- 2! = 2 * 1! = 2 * 1 = 2
- 3! = 3 * 2! = 3 * 2 = 6
- 4! = 4 * 3! = 4 * 6 = 24
- и т.д.
Итак, факториал числа 0 равен 1, и это важное математическое свойство, которое используется в различных областях науки и техники.
Определение и свойства
Факториал числа натурального числа n обозначается как n! и определяется как произведение всех натуральных чисел от 1 до n включительно. Если n = 0, то по определению, факториал 0 равен 1.
Свойства факториала включают:
- 1! равен 1;
- n! равен произведению числа n и факториала предыдущего числа (n-1)! для любого натурального числа n > 1;
- (n+1)! равен произведению числа (n+1) и факториала числа n! для любого натурального числа n.
Эти свойства позволяют рекурсивно вычислить факториал большего числа, используя факториалы меньших чисел. К примеру, чтобы вычислить факториал числа 5, мы умножаем 5 на факториал числа 4, который в свою очередь равен произведению 4 и факториала числа 3 и так далее.
Факториал
Например, факториал числа 5 равен 5! = 5 * 4 * 3 * 2 * 1 = 120.
Однако, возникает вопрос, каков должен быть факториал числа 0?
По определению, факториал числа 0 равен 1. Это странно и непривычно, но есть несколько объяснений, почему такая конвенция была установлена.
Во-первых, можно рассматривать факториал как способ подсчета числа перестановок. Если у нас есть пустое множество элементов, то оно имеет только одну перестановку — пустое множество само по себе. Таким образом, его факториал равен 1.
Во-вторых, математические формулы и идеи, связанные с факториалом, более элегантно работают, когда факториал 0 равен 1. Например, формула для биномиальных коэффициентов (C(n, k)) включает в себя вычисление факториалов, и она будет работать только при условии, что факториал 0 равен 1.
Таким образом, хотя это понятие может быть неочевидным или неприятным, факториал 0 равен 1 и используется в математике и приложениях, связанных с комбинаторикой и перестановками.
Интересные примеры и приложения
Факториал нуля, который обозначается как 0!, определен как произведение всех положительных целых чисел от 1 до 0, и в общем случае равен 1. Это может показаться непонятным и неочевидным, но в математике такое определение имеет свои основания и применения.
Одно из интересных приложений 0! находится в комбинаторике. Комбинаторика изучает способы комбинирования объектов. Например, если у нас есть некоторое множество из n различных элементов, и мы хотим выбрать из него все возможные подмножества, то общее количество подмножеств будет 2^n. Интересно, что это утверждение выполняется даже при n = 0.
Другое интересное применение 0! находится в области математического анализа. Оно связано с понятием экспоненциальной функции и ее рядом Тейлора. Ряд Тейлора позволяет разложить сложные функции в более простые компоненты — и это разложение особенно полезно в случае, когда мы работаем с экспоненциальной функцией. Найдя ряд Тейлора для экспоненциальной функции и произведя все необходимые вычисления, мы получим выражение, где факториал нуля равен 1.
Таким образом, 0! играет важную роль в математике и имеет различные приложения в разных областях. В то время как его определение может показаться необычным, оно имеет строгие математические основания и позволяет проводить различные рассуждения и вычисления.
Объяснение и доказательство
Факториал числа можно определить как произведение всех положительных целых чисел от 1 до данного числа. Согласно этому определению, факториал натурального числа n может быть вычислен следующим образом:
n! = n × (n — 1) × (n — 2) × … × 2 × 1
Доказательство этого факта можно провести следующим образом:
1. Рассмотрим определение факториала n!:
n! = n × (n — 1) × … × 2 × 1
2. Вспомним, что умножение числа на 1 не изменяет его значение:
1 × n = n
3. Тогда, если n = 1, можно записать:
n! = n × (n — 1) × … × 2 × 1 = 1 × (n — 1) × … × 2 × 1
4. Однако, если n = 1, факториал выражается следующим образом:
1! = 1 × 1 = 1
5. Сравнивая это выражение с предыдущим, мы видим, что получается:
0! = 1
Основное объяснение
При определении факториала числа 0 возникает некоторая парадоксальность: не смотря на то, что на первый взгляд кажется, что нечего умножать, факториал 0 равен 1.
Существует несколько объяснений этого феномена:
- Одно из объяснений основано на комбинаторике и связано с пустым множеством. Так как у нас нет ни одного элемента для умножения, мы можем считать, что это пустое множество и его факториал равен 1.
- Другое объяснение связано с аналитическими функциями и рядом Тейлора. Формально, мы можем рассматривать функцию f(x) = 1 / (1 — x) и разложить ее в ряд Тейлора в окрестности x = 0. Ряд будет иметь вид: f(x) = 1 + x + x^2 + x^3 + … . Подстановка x = 0 в этот ряд даст нам f(0) = 1, что соответствует факториалу 0.
В любом случае, факториал числа 0 равен 1 по соглашению и стандартным математическим конвенциям. Это значения, которое используется во множестве математических формул и вычислений.
Математическое доказательство
Существует несколько математических доказательств, которые подтверждают, что факториал нуля равен единице.
Доказательство на основе комбинаторики:
- Рассмотрим множество всех возможных перестановок нуля элементов.
- Первая и единственная перестановка в этом множестве будет пустым множеством.
- Согласно определению факториала, количество перестановок нуля элементов равно факториалу нуля.
- Таким образом, исходное множество содержит одну перестановку.
- Следовательно, факториал нуля равен единице.
Доказательство на основе рекурсии:
- Факториал представляет собой произведение всех натуральных чисел от 1 до данного числа.
- При рекурсивном определении факториала факториал нуля можно считать базовым случаем.
- Если факториал нуля равен 1, то формула для определения факториала:
- n! = n * (n-1)!
- остается согласованной, так как n! = n * (n-1)! = n * 0! = n * 1 = n.
- Следовательно, факториал нуля равен единице.
Вопрос-ответ:
Зачем вообще нужно знать, что 0 факториал равен 1?
Знание того, что 0 факториал равен 1, является основой для многих математических выкладок и формул. Это понятие активно используется в комбинаторике, алгебре и анализе. Кроме того, это свойство выигрывает важную роль в теории чисел и квантовой физике.
Как объяснить почему 0 факториал равен 1?
Существует несколько способов объяснить, почему 0 факториал равен 1. Возможно, самый простой из них заключается в использовании рекурсивной формулы для вычисления факториала. Если применить эту формулу к числу 1, то получим 1! = 1 * 0!. Перенесем 0! в левую часть и разделим обе части на 0, получим уравнение 0! = 1. Таким образом, мы приходим к выводу, что 0 факториал равен 1.
Можно ли посчитать 0 факториал с помощью комбинаторики?
Да, можно. В комбинаторике факториал обычно интерпретируется как количество способов перестановки элементов множества. И чтобы рассчитать количество способов перестановки пустого множества, необходимо учитывать, что пустое множество можно переставить только в одном порядке — самом себе. Таким образом, мы приходим к выводу, что 0 факториал должен быть равен 1.
Можно ли привести какой-нибудь пример, чтобы наглядно показать, что 0 факториал равен 1?
Да, можно привести пример с помощью комбинаторной интерпретации факториала. Рассмотрим задачу: сколькими способами можно разложить набор из 0 элементов? Ответ очевиден — единственным способом, именно этот набор сам себе соответствует. Таким образом, мы приходим к выводу, что 0 факториал равен 1.